interactive analog LED wave array
microcontrollers are overrated
introduction
This is an LED array that lights up in response to motion and sends waves across the array. The array consists of identical "units" connected in a grid, with 16 units per board. Boards are tileable to make an arbitrarily large array.
What makes this array unique is that the LEDs are controlled entirely by analog circuitry. No digital logic anywhere! (Except perhaps the switching regulators on each board.) All "computation" is done by operational amplifiers (opamps). There is no need for it to boot up or communicate with anything else, and the dimming and wave effect are completely smooth with no modulation or discrete levels.
concept and design
A Long Time Ago(TM) I was curious about the uses of opamps. I learned that they were capable of implementing many mathematical operations, including differentiation and integration. It also happened that I had recently learned about differential equations, which can be solved by (you guessed it) differentiation and integration. Putting two and two together...
I got the idea to visualize differential equations using an array of LEDs and motion sensors driven by opamps. I wanted to create a circuit to model a physical process by solving a differential equation, like the wave equation or the heat equation. In particular, I thought the wave equation would be fun; waving your hand over the array would be like stirring a pool of water.
This idea then languished for some ten years.
math (danger: math)
note: this section requires JavaScript to display properly.
Translating a differential equation into a circuit requires some math, but fortunately it's not as complicated as it looks.
Fundamentally, a (scalar) wave exists in a scalar field - a quantity like height, temperature, or intensity that varies over space and time. This field can be described by a function \(u(\textbf{x}, t)\) of (possibly multidimensional) space \(\textbf{x}\) and time \(t\). The wave equation describes how an ideal wave propagates in a scalar field; it is the second order partial differential equation $$ {\partial^2u \over \partial t^2} = c^2 {\partial^2u \over \partial\textbf{x}^2} $$ It states that the second time derivative, or "acceleration", of the field's value at any one point is proportional to its second space derivative (roughly speaking, the curvature) at any point, with the constant \(c\) controlling the speed of acceleration and thus wave propagation.
Opamps can integrate and differentiate continuously over time, but because the array consists of discrete units in a square grid, we have to approximate the second derivative in space. There are several ways to do this. The method used here is the discrete Laplacian on a five-point stencil, which is a fancy way of saying "find the difference between a point and the average of its four direct neighbors".
Substituting the discrete second derivative and considering value at a single point \(u_\textbf{x}(t)\), the wave equation becomes $$ {d^2u_\textbf{x} \over dt^2} = c^2 (u_1 + u_2 + u_3 + u_4 - 4u_\textbf{x}) $$ with \(u_1, u_2, u_3, u_4\) being the values at each of the four neighbors. This is the equation that each unit solves, by integrating twice over time.
For a physical analogue, imagine a horizontal grid of point masses that are each constrained to move vertically, connected by springs. This forms a 2D discrete scalar field where the height of each point is its value. Any single point mass will remain stationary if there is no net force on it - in other words, if forces trying to pull it up are exactly balanced by forces trying to pull it down. This is the case if the height of the point is equal to the average heights of its neighbors. If a point is higher than the average of its neighbors, the springs will try to pull it down, and vice versa. The greater the difference is, the stronger the force, which is proportional to acceleration.
theory to reality
It's relatively straightforward to put together an opamp circuit to solve the above, but the details can be tricky. After much time with circuit simulators and even more time with a few prototypes, I had a circuit suitable for production.
The circuit I came up with is a grid of "wave units", each containing one quad opamp, a white and a blue LED, and a bunch of resistors and capacitors. One board consists of 16 of these units, with each one connected to its neighbors directly on the board or via edge connectors. The edge connectors can also be used as a general interface for driving the array.
Each board has eight IR LED/photodiode pairs that sense motion. Each pair drives two adjacent units. I considered using one sensor per unit, but the extra resolution is not necessary and the relatively tall T1 packages of the IR LED and photodiode would obscure the flat surface mount LEDs if placed too close.
The boards take 10-15V DC power through the edge connectors or the optional barrel jack or screw terminals. There is a buck regulator on each board that converts the input voltage to 4.5V for the circuitry. (This specific voltage is important, as explained below.)
circuit details
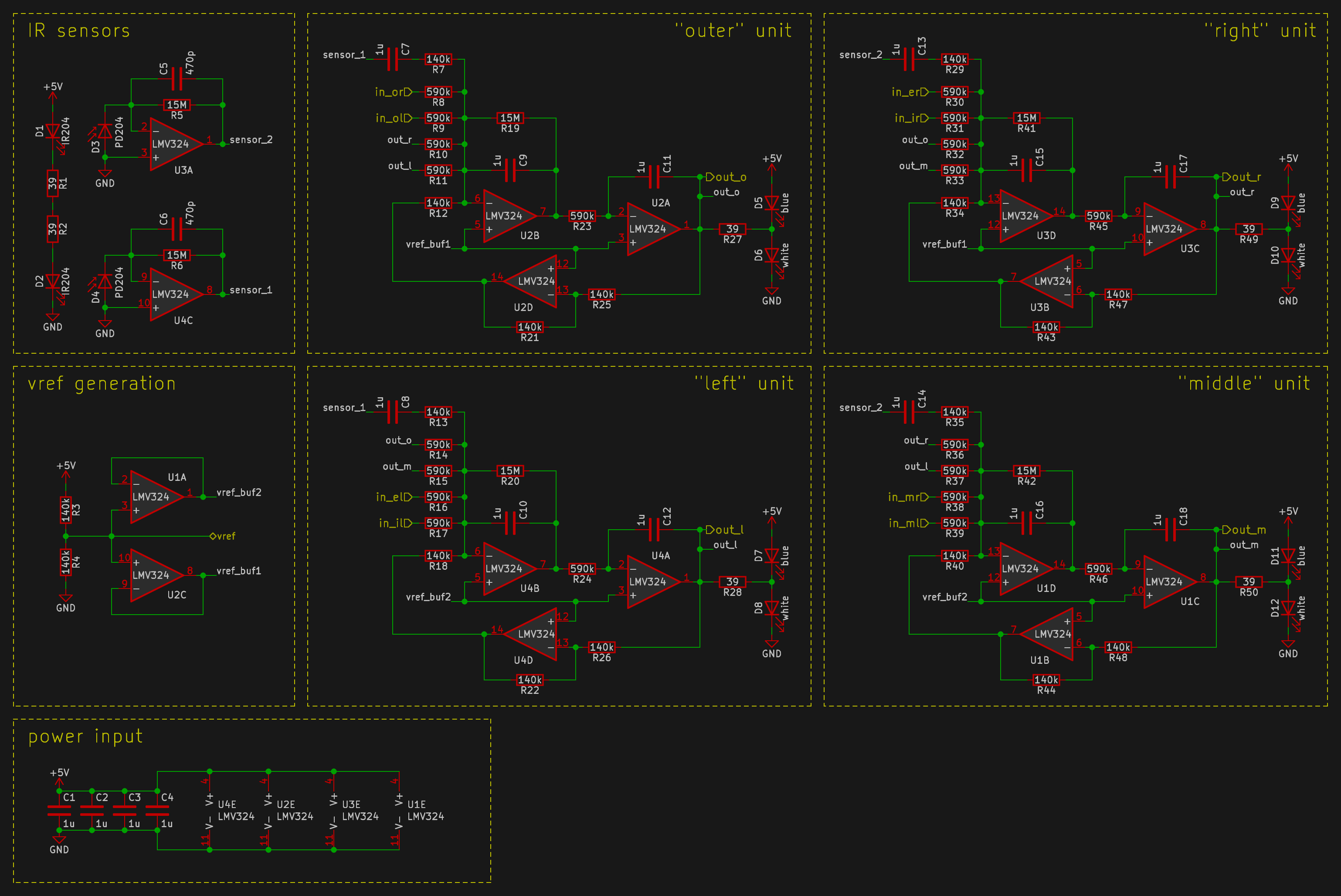
Each board is made up of 16 identical units plus some supporting circuitry. A unit has four opamps, three of which are used for the wave logic and the last of which is used for other purposes. For convenience, the 16 units are divided into four quarters with 4 units each:
do the wave
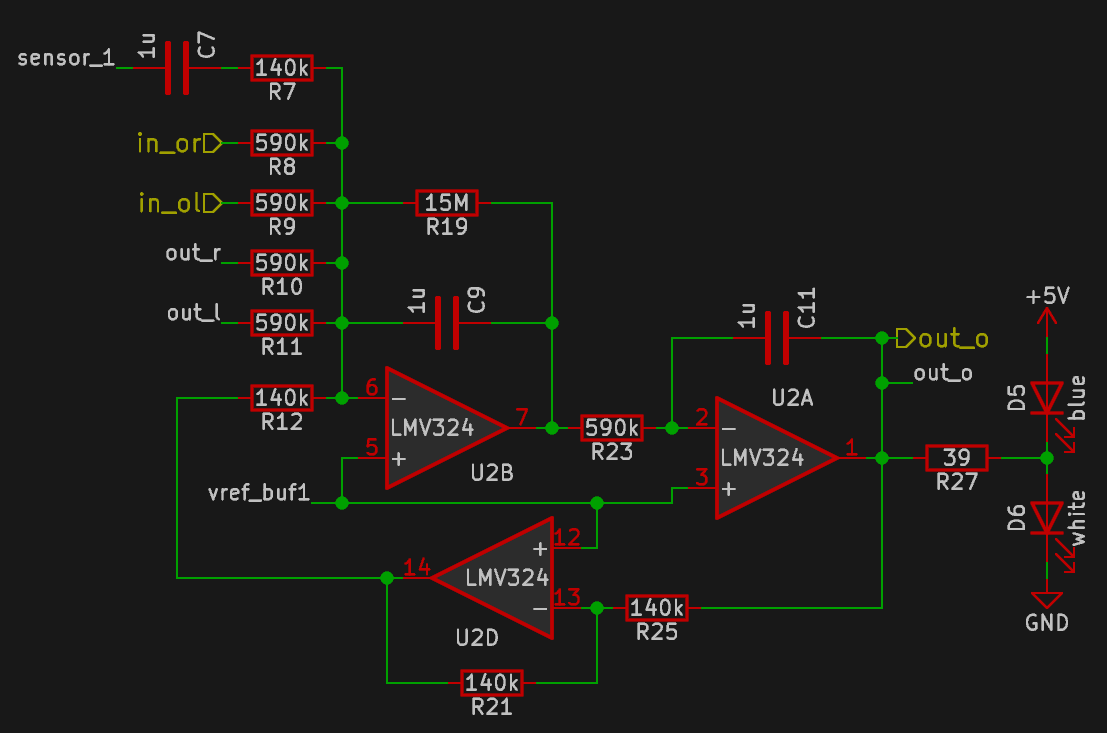
The 16 wave units are all the same, so we will focus on one unit:
Each unit consists of three parts: a summing integrator, a plain integrator, and an inverter.
Opamp U2B and its supporting components form the (inverting) summing integrator. Inputs from the four neighboring units come in through the 590k resistors R8-R11 to sum with the inverted feedback coming through 140k resistor R12. This assigns the feedback approximately four times the "weight" of the inputs from the neighbors. The sensor input is also fed in here through resistor R7, with capacitor C7 blocking DC voltage to ensure that only motion will cause the array to light up.
The 1uF capacitor C9 creates the integrating behavior. The 15M resistor R19 provides damping with a time constant of 15s, ensuring that the waves will dissipate eventually.
Opamp U2A is an inverting integrator with a time constant of 590k * 1uF = 0.59s, set by R23 and C11. The inversion of this integrator cancels the inversion of the previous integrator. Notably, this integrator does not require a resistor across the feedback capacitor as the overall negative feedback prevents this integrator from drifting.
Opamp U2D and resistors R21 and R25 form a simple unity gain inverting amplifier to negate the output so the feedback from the unit is subtracted by the summing integrator.
The output of U2A (the "value") is fed into the LEDs, which are in series across the supply rails. In the quiescent state, the midpoint of the LEDs is held at the reference voltage (half the supply voltage). With the 4.5V supply voltage, the 2.25V across each LED is barely below the voltage at which they light up noticeably. This way, driving the midpoint high will light up up the low side LED and driving it low lights up the high side LED. Combined with the LEDs' exponential response, this provides a sensitive and smooth visible output.
This arrangement has the drawback that it is sensitive to LED forward voltage, so the supply voltage must be adjusted for different colors of LED, and it works best when the two LEDs have roughly the same forward voltage. White and blue pair well (white is simply blue with a yellowish phosphor); other phosphor LEDs (pink and purple) should also work with the same supply voltage.
supporting cast
Each unit has a sensor input and a reference voltage input, which are supplied by these bits:
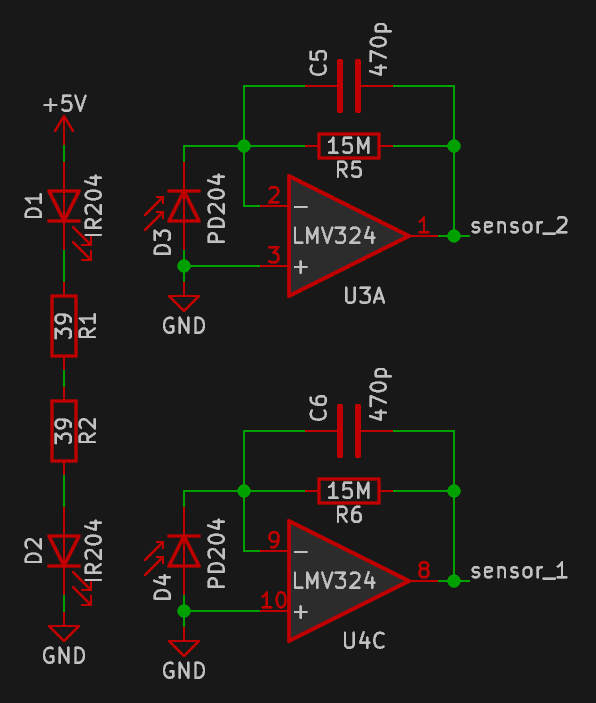 |
The sensors consist of infrared LED (D1, D2) and photodiode (D3, D4) pairs. Each LED is next to a photodiode, which use half of the remaining opamps (U3A, U4C) as transimpedance amplifiers (current to voltage converters) with a gain of 15Mohm set by R5 and R6. Capacitors C5 and C6 reduce noise by creating a low-pass filter with a cutoff of about 22Hz, which is low but still comfortably above even the most frantic hand-waving. |
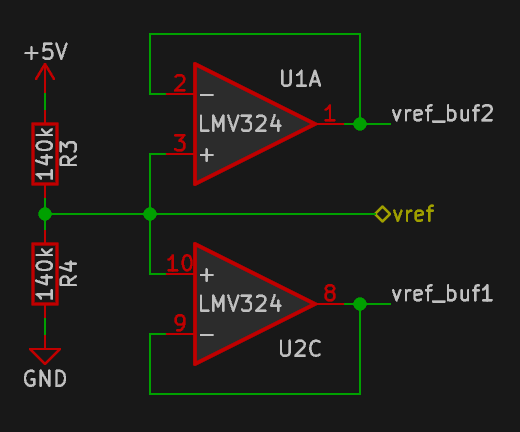 |
Because the opamps are run off a single-ended supply, they are referenced to half of the supply voltage to allow both "positive" and "negative" voltages. This reference is generated by a resistive divider R3 and R4, and buffered by the remaining opamps U1A and U2C. All four dividers on one board are also connected to each other for a uniform reference voltage. |
realization
So far we've gone from arcane thoughts in head to arcane symbols on (electronic) paper to different arcane symbols on paper. Now it's time to make some boards.
layout
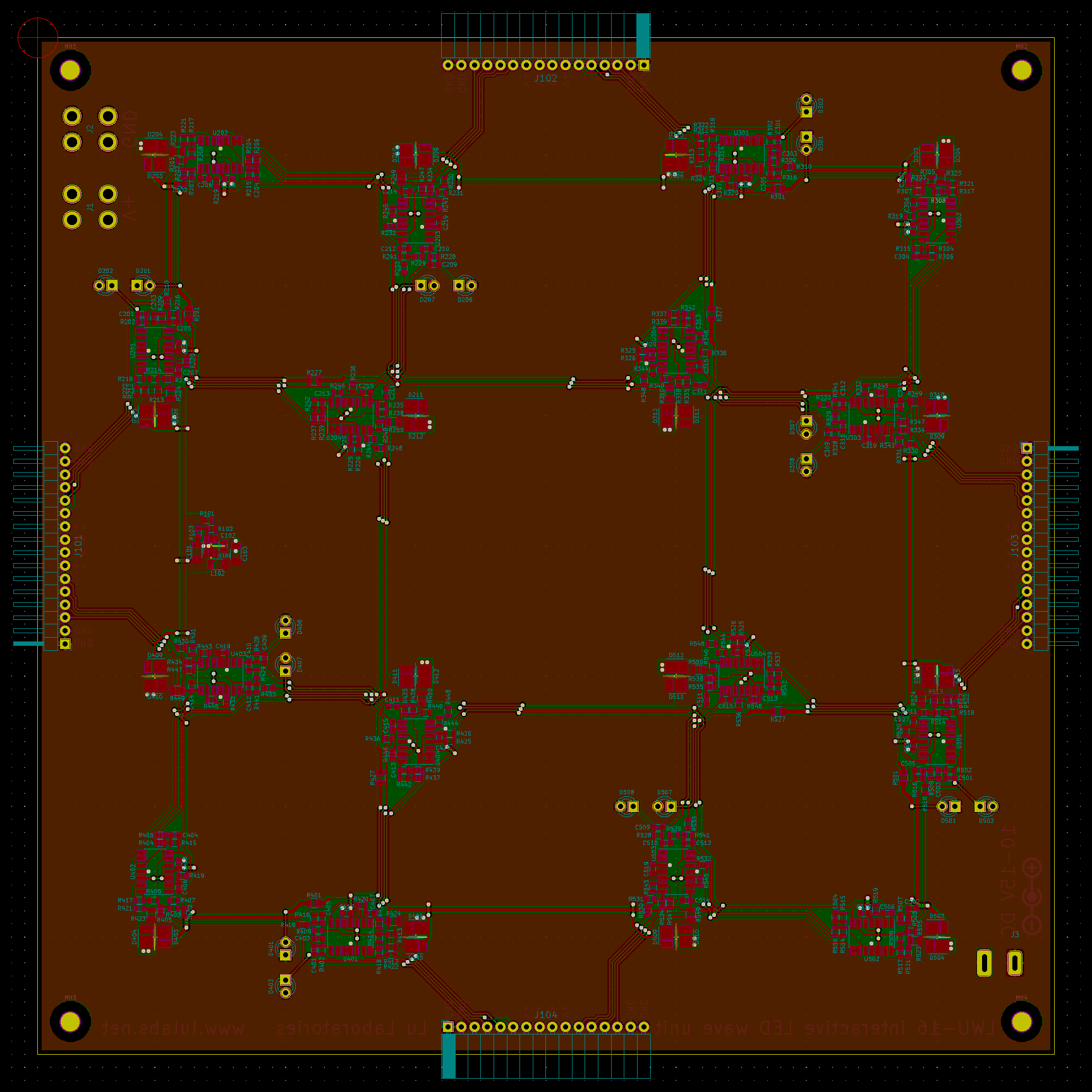
I used KiCad to draw the schematic and lay out the board. KiCad is bestcad.
The board is a simple 2-layer board with a ground plane on the bottom and power fills on top. It is rotationally symmetric with the exception of the voltage regulator, so I laid out one quarter of the board manually and then used a script to copy and rotate the layout for the other three quarters.
Units are arranged such that the white/blue LED pairs form a square grid with 2" (50.8mm) spacing, which means that boards are on a 8" (203.2mm) square grid. Each board is 7.8" (198.12mm) square, leaving a small gap between boards when assembled.
Input power is routed to all four edge connectors and the auxiliary power connectors via a ring of copper pour around the edge. Supply voltage for the circuitry is routed via the inner copper pour, separated from the outer ring by signal lines between the units.
Sensors are placed halfway between adjacent units and offset slightly for more even coverage.
manufacture
The boards were made and assembled by PCBWay. They looked excellent, but they did not work out of the box. I suspected that this was my fault, so I started debugging.
It did not take long to find the issue. The board was designed to use the AP65111A switching regulator, which was unavailable at the time due to supply chain issues. I chose to substitute it with the AP65211A, a switching regulator from the same product line in the same package; the only difference appeared to be that it was rated for 2A output instead of 1.5A. I missed the fact that it also has a completely different pinout. Oops. Diodes Inc., if you are reading this, it's not really your fault, but please make products in the same product line with the same basic functionality and the same package also have the same pinout.
Fixing the boards is simple but tedious - remove the offending chip and replace it with the correct one, on each of 100 boards. (I am lazy, so only the 25 boards in use are fixed as of writing this.)
PCBWay added rails to two opposite edges of each board with fiducials (alignment markers) and did not remove them before shipping. I would have been happy to add the fiducials to the layout so they would not have to add rails, but was not informed about this requirement beforehand. I was also under the impression that the rails would be removed by default as the prototype they manufactured did not have rails. It could be that the smaller prototype boards were panelized, or went through some other manufacturing process. Fortunately, the rails are thinner than the planned gap between boards, so the boards fit together even without removing them.
assembly
finished array
It makes for a fun decoration mounted on the wall of my kitchen. I enjoy playing with it any time I walk by. It also reacts to the direct sunlight it sometimes gets in the afternoon, adding some gently varying light to the room. The room lights don't faze it as they are all LEDs with essentially no near-infrared emission.
At idle, the array of 25 boards draws ~18W from the wall, increasing to ~70W when fully active. It is difficult to fully activate all the units just using the sensor input, but because of the offset reference voltage, they are all fully on right after power is applied.
The waves don't propagate quite like I would expect. They seem to have a higher phase velocity than group velocity - the peaks and troughs advance faster than the front of the wave. I suspect that it's because the discrete approximation of the second derivative isn't entirely accurate. There should also be some additional non-ideality because the ceramic capacitors used change capacitance with applied voltage. I would expect it to manifest as faster waves at higher amplitude, but the effect is small at the voltages involved and it's hard to tell.
Those non-idealities don't matter though; a perfect ideal wave would be pretty boring. Non-ideal behavior makes the array more dynamic and fun!
 top level
top level